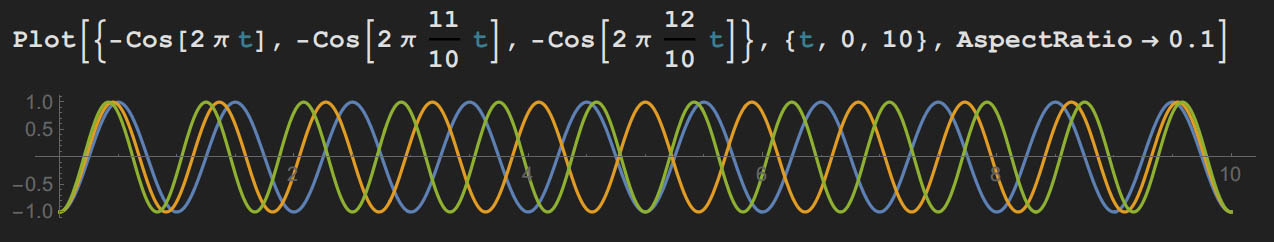$ \newcommand{\uni}[1]{\ \mathrm{#1}} \newcommand{\E}[1]{\times 10^{#1}} \newcommand{\ket}[1]{|#1\rangle} $
(本次只选了六张图,每张图的篇幅都比较长应该可以弥补吧 _Σ:з」∠)_ )

原理:
这张图中的现象在
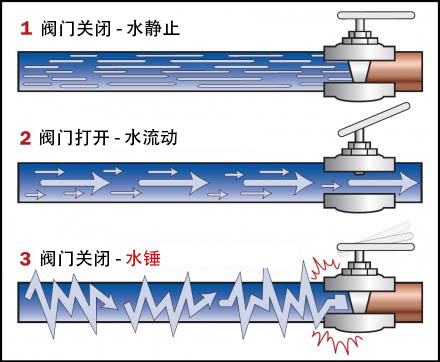
《 What-if 第六期:半空的杯子》 中提到过。找一个玻璃瓶,装上一些水,狠击瓶口,于是瓶体在短时间内获得向下运动的速度,但瓶中的液体由于惯性没有跟上瓶纸的步伐(水的黏度很小),就在瓶底形成大量接近真空的低压气泡,这一现象的术语叫做空化(cavitation)。然后瓶外的大气压就想把水往瓶底压,同时还受自身重力开始奋力往下追,由于液体不太容易被压缩,所以力最后都啪唧拍到了瓶底上。标准大气压约为 101 千帕,相当于 81 千克的重力砸在直径 1 分米的瓶底,妥妥地把瓶底压破啦。
展开 Mathematica 代码
101325*\[Pi]*0.05^2/9.8
= 81.2046
花絮:
xkcd 把这种现象叫做“水锤”,有时关上水龙头时听到 Duang~ 的一声就是水锤的作用。
危险:
↗ 某种虾就是利用前肢高速出击产生的空化束流来攻击猎物的,愚蠢的人类,捅穿玻璃缸你怕不怕。

刚看到 这篇论文 的标题时其实我是拒绝的,“Tip Singularity”?尖端奇点?然后又看到“Freezing Water”,冰水结晶时的奇点?不会是低温凝聚态领域的什么高深的现象吧,那我可写不来……
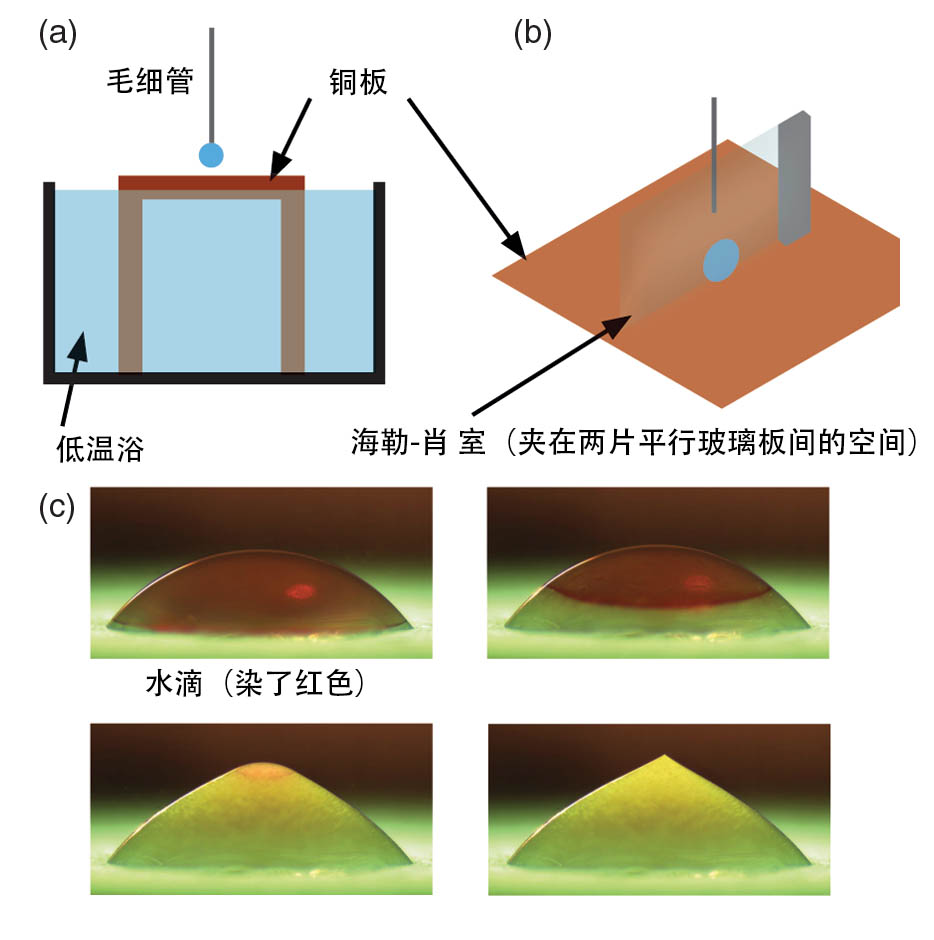
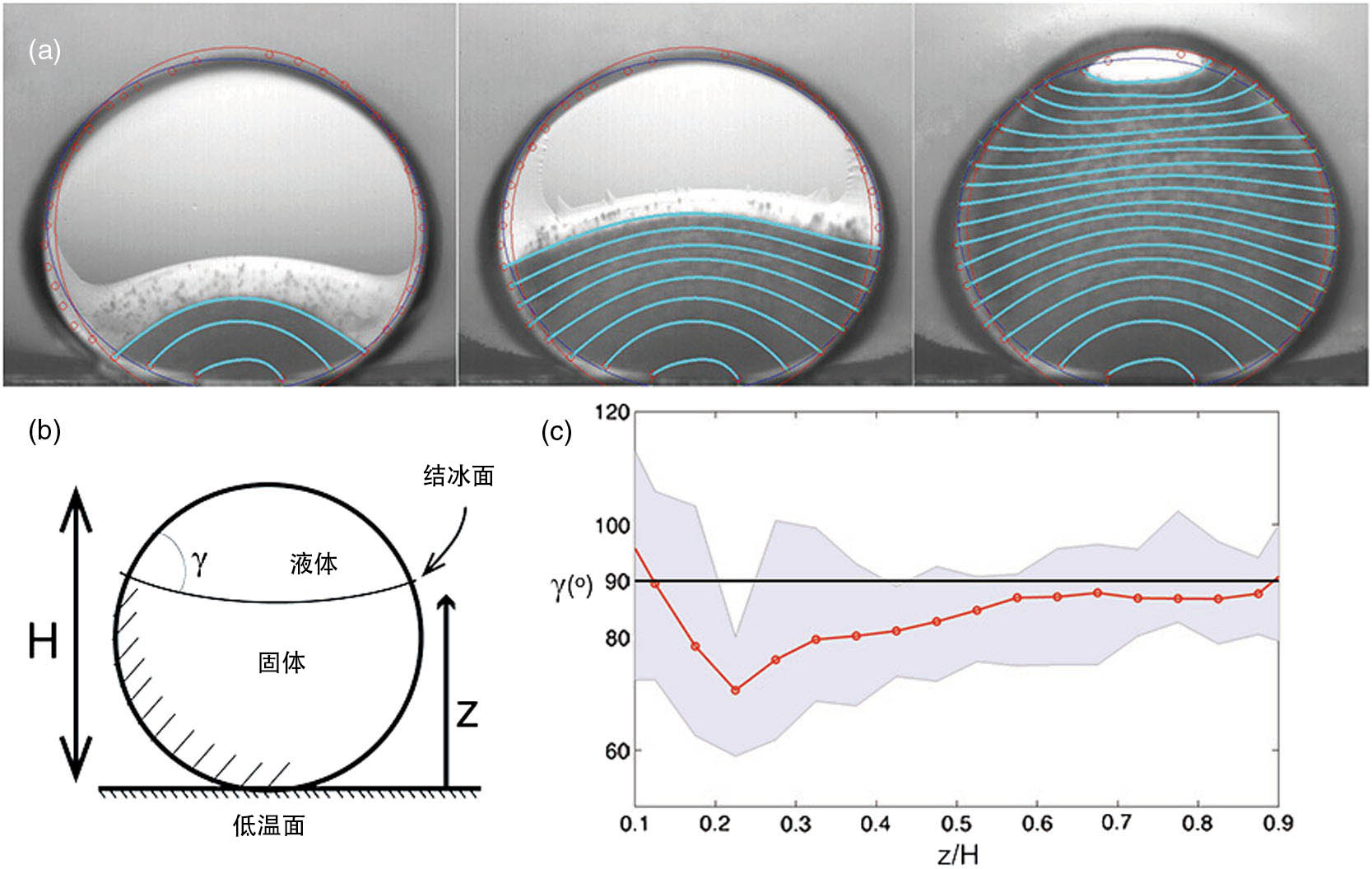
然后看完摘要后我释然了,这个标题应该译为“水滴结冰普遍形成尖顶现象”,就是说水滴在冰冷的表面结冰时,最后总会形成一个尖尖的锥形的顶部。研究者把水滴滴在两块平行的玻璃板之间,然后拍摄它结冰的截面图,从而避免了球形水滴会使画面扭曲的问题。他们的结论是最后形成的锥尖的顶角与液滴的大小无关,与底板的温度或浸润角(液体表面和容器壁接触时形成的角度)无关,与结冰的速度亦无关,因此这个现象是普遍的。论文随后定量地推导了锥顶角的大小(131°),理论和实验结果相符(139°±8°,两百多次实验)。
原理:
在这篇论文以前,人们定性的解释就是水在结冰是体积会增大而已。这篇论文的主要贡献是改进了以前的热传导模型,推导出了一个定量的结果,那就是结冰面总和液滴表面成 90° 左右(下图中的 γ 角),因此它往上推进时就会由凸变凹,最终收出一个尖顶出来。也就是说,尖顶现象主要是几何上的结果而非动力学效应。
花絮:
由于这个模型是普适的,作者在论文最后展望这项研究对飞机机翼的结冰过程,以及 3D 打印的凝固过程会有帮助。
危险:
他们说这是一个“务必在家中尝试”的实验('do try this at home' experiment)2333

《男孩和他的原子》是 IBM 在 2013 年发布的一部“世界上最小”的定格动画,影片长约 45 纳米,宽约 25 纳米,用一台两吨重的扫描隧道显微镜在 5 开氏度的低温下将一氧化碳分子排列在铜基板上,总共扫描了 242 张图片,构成了这段一分多钟的电影,花费 4 位研究员 2 周时间制作完成。完整电影可在 此处下载。
原理:
这种能看到原子的图片并不是用多么强大的光学手段拍摄而成的,而是用一个极细的针尖在材料表面“摸”出来的。针尖也并非直接和材料表面接触,而是悬空了很小一段距离,此时你在材料和针尖之间加上电压的话,就会有微弱的电流流过(在量子力学中叫作隧穿电流),并且这一电流的强度对针尖和材料表面的距离十分敏感。因此我们就可以慢慢地移动针尖(针尖的移动当然也不是用齿轮,如此微小的移动用的是压电陶瓷,一种加电压后长度会微小变化的材料),如果测到电流开始增强,说明我们在接近一个凸起的表面,于是我们就把针尖调高一些,让电流回到原来的大小。这样保持电流大小不变不断调整针尖的高度一路扫描下来,我们就能得到材料表面的高度图。
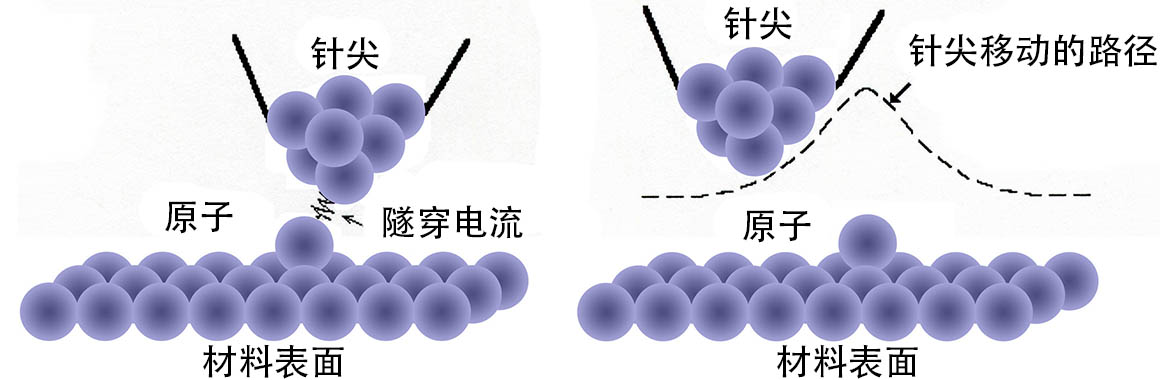
以上讲的是 STM 的恒电流工作模式,另外还有恒高度工作模式,即保持针尖高度不变,然后根据隧穿电流大小的变化得到材料表面的高度,这种模式的优点是扫描速度快,缺点是有可能碰坏针尖。
针尖既然能“摸”出原子,当然也能移动原子,移动的方法有横向操纵和纵向操纵两种。横向操纵是调高隧穿电流,然后针尖就会吸着原子在材料表面走,原子并未脱离材料表面。纵向操纵则是把原子提起再放下,一般是通过加强电场然后改变电场的极性来实现。
花絮:
除了这部电影外,团队还为《星际迷航》系列电影制作了三张图片,分别是《星际迷航》的标志、瓦肯手势、以及世界上最小的企业号手办:


【这张图是加长版的请编辑注意一下】
有字幕组已搬运了 完整的视频。高中学理科的童鞋大概没少算过电子在电磁场中偏转的题吧,这就是显像管(CRT)的原理,首先阴极发射出电子束,在阳极的吸引下加速,然后在电磁场中偏转指定的角度,最后打在荧光屏上发光,不同能量的电子可激发出不同颜色的光,形成电视屏幕上的彩色图像。
原理:
大块钕磁铁
【这个字是钕(Neodymium)不是铷,请编辑注意】能产生很强的静磁场,根据磁铁正面在电视机上制造的画面我判断这个磁铁是轴向磁化的,磁铁的两面分别把画面推到右上角和右下角的受力分析图:
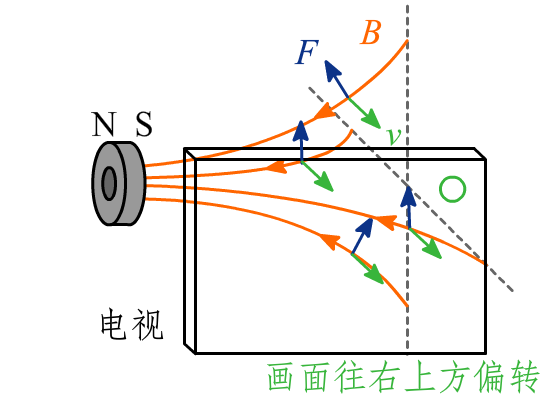
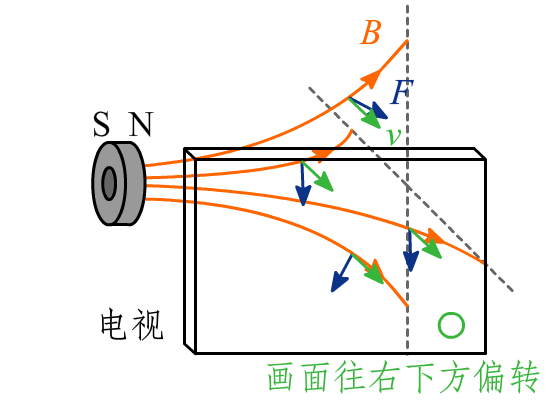
磁铁贴到屏幕表面时形成白点的原因:
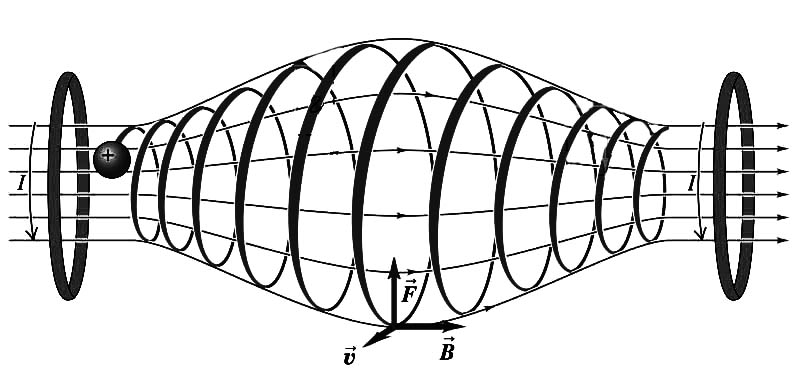
这个现象叫作磁瓶(magnetic bottle),带电粒子往磁感应强度增大的方向运动时回旋半径会跟着缩小,它的证明我曾经留给读者作练习来着。
视频中还可看到另一块小磁铁贴到屏幕表面时形成的是一片黑域,这是因为那块小磁铁的磁化方向和前面讨论的钕磁铁不一样,我判断它是沿径向磁化的,所以它正面贴到屏幕上的效果实际上相当于钕磁铁侧面时的排斥效果,这也能解释小磁铁翻面后的效果一样。【这段去掉吧篇幅太长】
花絮:
小时候拿磁铁在电视屏幕上玩结果把电视画面玩坏了的一定不止我一个 (→_→)。有外国网友说他在一侧把电视玩坏后,把磁铁放另一侧玩试图把画面调回来…… 于是后来他成了电子及计算机工程师 2333。
电视画面有误差的原因是电视内部的一些金属器件被永久磁化了,正确的修复方法是消磁(degauss),有的电视机自带这个功能,即产生一个方向快速变化的磁化场,然后磁化场的强度慢慢减弱,最后任何方向的剩磁都被抹平了。
危险:
强磁铁是危险物品,你要没点臂力根本把持不住。如果你手里拿着这货然后它把附近什么东西吸过来了(比如另一个磁铁),那效果就跟一锤砸在手上一样。

(壕会玩系列 【磁铁夹碎 Apple Watch】 视频)

原理:
电磁炉的工作原理是电磁感应加热。电磁炉首先将市电转化为高频交流电(20~40 kHz,对于交流电属于高频,但对于无线电波属于低频,所以电磁辐射少),然后交变电流通过线圈建立交变磁场,交变的磁场感应出涡旋的电场,此时将导体放在线圈上的话就会形成涡电流,涡电流流过导体时因电阻产生焦耳热。诸如空气、蛋白质、陶瓷等非导体有很高的阻抗,因此电磁炉几乎不在它们上面输出功率。所以直接把鸡蛋打在电磁炉上是热不了的,陶瓷或玻璃锅也是加热不了的。
花絮:
原理上,电磁炉可以加热所有导体锅,但市面上的电磁炉仅适用于加热铁锅(以及不锈钢等具有铁磁性的锅)。 铁锅的特点是导磁性强,漏磁少,并且除了涡电流之外还有磁滞损耗效应(即上一张图中提到的转着方向磁化的过程,那个过程是会放热的)来产热,因此使用铁锅有更高的加热效率。
而铜或铝不行的原因是电阻太小了(高中学理科的童鞋应该体会过阻抗匹配,即外电路电阻和电源内阻相等时输出功率才最大,太大或太小都不行)。铜铝的趋肤效应(交变电流喜欢贴在导体表面流动的现象)比铁弱,意味着涡电流在锅底流通的厚度更宽,所以阻抗更小,加热效率更低。市面上的电磁炉都是为铁锅设计的,如果要加热铜铝的话需要设计不同的工作频率。实际上,实验室中使用的感应电炉就有多种频率可供选择。
危险:
电磁炉应远离收音机、电视机、手表、磁带、铁质的餐具等。携带心脏起博器及佩带磁疗仪的人应慎用电磁炉。勿将电磁炉放置在燃气灶附近使用(可能会将燃气灶的铁质金属件加热),安全起见也不要放在任何金属平台上使用。(资料来源:各品牌电磁炉的说明书)
危险:
请勿在乘坐公共交通工具时观看此图,以免坐过站。(← 嗯,因为很危险所以要把这句话放在图片前面)

原理:
图中现象叫作蛇摆(pendulum wave,我也不造为啥会翻译成蛇摆),我们知道单摆的周期的公式为 $2\pi\sqrt{L/g}$,然而解释蛇摆现象并不需要这个公式(如果你要动手做一个蛇摆的话才需要),我们只需要关注各个摆的周期即可。
蛇摆是这么设计的:首先设定一个蛇摆整体恢复的大周期 $T$,然后让最长的摆在 $T$ 内摆比如说 10 次,那么次长的摆就在 $T$ 内摆 11 次,次次长的摆 12 次… 以此类推,每个摆各自的周期是 $T/(10+n)$。下面我们先以三个摆为例画一张位移-时间图(横轴是时间,纵轴你说是位移或者摆角都行)
展开 Mathematica 代码
Plot[{-Cos[2 \[Pi] t], -Cos[2 \[Pi] 11/10 t], -Cos[
2 \[Pi] 12/10 t]}, {t, 0, 10}, AspectRatio -> 0.1]
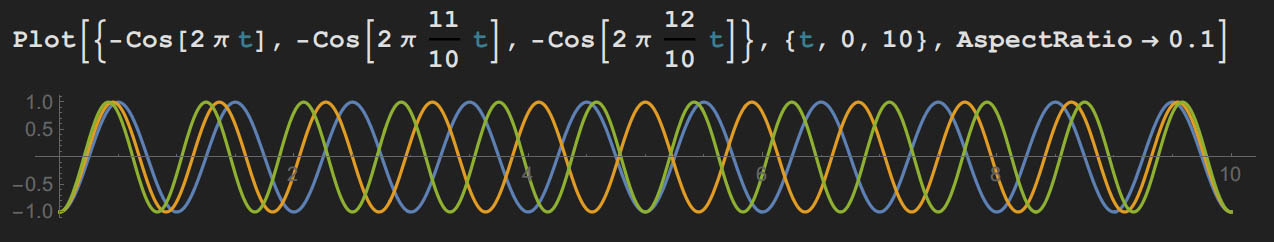
只用三个摆就可以看出,在半个大周期的时刻有一个分组现象。这不难理解,在 $t=T/2$ 时各小球摆过的路程是 $(10+n)/2$,因此 $n$ 为偶数的球都整除,而 $n$ 为奇数的球都正好余半个周期。
很好,上面动图中的蛇摆是是 15 个球的(我数了好几次你造吗),那么我们就画它 15 个 cos 函数:
展开 Mathematica 代码
T = 12;
Plot[Table[-Cos[2 \[Pi] n/T t], {n, T, T + 15}], {t, 0, T},
AspectRatio -> 0.1, PlotStyle -> Thin, Frame -> True,
FrameTicks -> {Table[12/m, {m, 1, 12}], {-1, 0, 1}}]
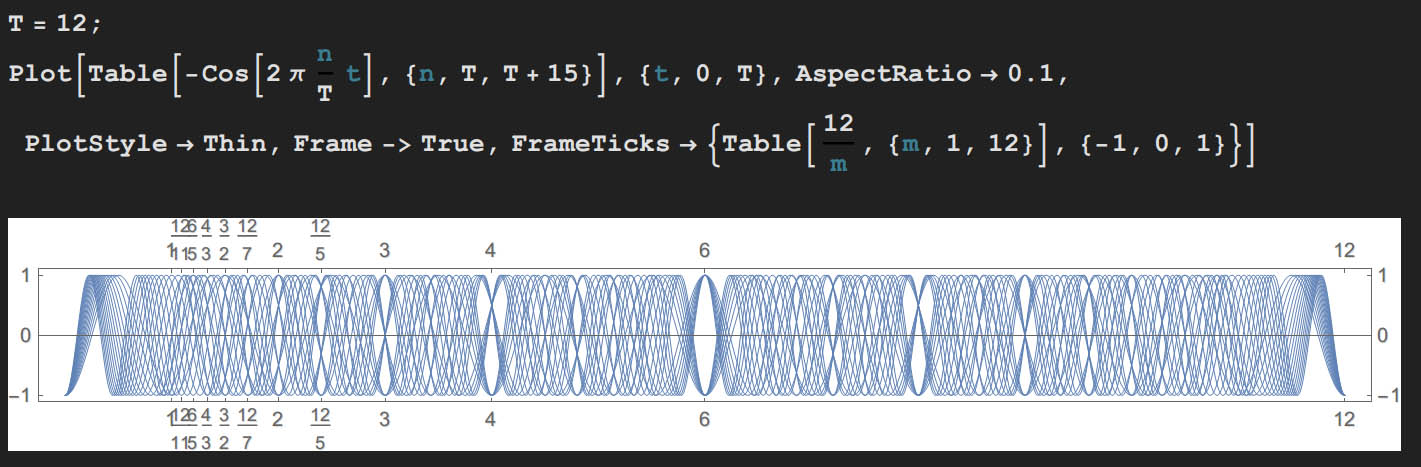
我选了个因子多的整数 12 作周期,并按分数倍周期标注了横轴,这样你们就能看出分数恢复的现象了。分数恢复和半周期恢复的原理类似,用数论的语言来解释就是,在每个分数周期,属于相应同余类的号球会恰好摆完相同的进度。例如在 $t=T/3$ 时,各小球摆过的路程是 $(12+n)/3$,因此按余数应分 3 组,只不过余 $2/3$ 周期的组折返回来刚好和余 $1/3$ 周期的组相遇,所以在该时刻会观察到小球整齐地排成了两排。
花絮:
分数恢复是存在量子化的体系特有的现象(这里只是借用了量子力学的术语,并不是说这个体系真的要用量子力学处理),如果你用无限多个摆连贯地排成一排(数学语言叫连续),那么你只会看到一条长蛇越来越密地铺满整个扇形面,看不到前面所讲的分组现象。